
Python有着各种各样的用处(网络,机器学习,深度学习,自动化,系统……),处理物理数据也有各种各样的软件和语言(Julia,Matlab,Mathematica,origin(蜗壳大雾推荐的,没用过),……)。作者最近在尝试用Python来处理一些基本数据,画个小图,还想要做一个小动画……
Begin
总之,我这个月入门大概做了这些事情:
- 大致学习了一下
numpy,scipy,matplotlib,mayavi - 处理了一下我的大雾(自由落体法——重力加速度拟合曲线)
- 画了一下电偶极子,电四极子的电势平面分布图
- 淑芬B2中几个二元函数的图形
- 整理了
matplotlib的一些最基本但够用的用法
事实上,这种想法源于某种比复仇更为严重和恐怖的动机:这实际上是要毁灭那些我们不能理解的事物—— 《Solaris》
为什么要可视化
可视化还是非常重要的。我们可以通过可视化来更好的认识大自然,直观的“看见”可以加强我们的物理图像;数学家们可以通过可视化来获得灵感;我们在日常生活中也离不开可视化(各种游戏,图形界面等等);同时,在研究中或新闻中利用可视化可以把数据具象化,使能受众可以更易接受。
Pros and Cons
首先来说一下为什么用Python来做这些事:
- Python中有专门开发的库,活跃的社区,完备的文档
- Python中的函数和功能也比较完备
- Python运行的速度远大于那些软件,也许对于轻量的计算软件更方便,但遇到更复杂的问题可能需要大量时间
- Python比较灵活,可以自己选择算法
- Python的兼容性强
- 不用学习新的语言
- 可以用Python来自己创造新的工具包
- 自己写可以增加对计算机的理解
- 可能是因为比较闲,不想卷绩点
- ……
But,诚如我的淑芬老师卿爷说:“一个人如果有一方面特别强,就有一个方面特别弱”
- 全部需要自己写,一开始不知道要干什么
- 看文档需要掌握一定技巧,否则会浪费一些时间
- 一开始效率较低,不如mma,matlab等来的爽快
- bugs
- ……
一个可视化的基本过程
我目前知道的画图的方法,也就是解数值解的方法。把自变量分为许多离散且接近的小量,然后再把它们画出来,最后便成了我们所看见的图。同样的,制作动画的时候也是把时间分为许多离散且比较接近的小量,也就是确定一个视频的帧数,之后就可以做成动画了。
库的介绍
大概说一下
| 包 | 大致功能 |
|---|---|
| numpy | 进行数据处理,创建数组(离散化) |
| scipy | 提供一些函数,进行一些运算 |
| matplotlib | 画图表,或制作动画(2D,3D均可) |
| mayavi | 主要是3D的渲染 |
| manim | 3blue1brown的动画引擎 |
Matplotlib的基本操作(笔记)
由于是笔记整理,可能说的不是很清楚,学习比较紧张,请大家见谅
并且一些接口参数会省略。
默认读者熟悉numpy。
大致是参考以下文章进行的学习
画图前的基本操作
1 | import matplotlib.pyplot as plt |
| 功能 | 方法 | 一些解释 |
|---|---|---|
| 创建画布 | plt.figure(figsize=(),dpi=,facecolor='',edgecolor='',frameon=) |
|
| 创建axes类 | fig.add_axes() |
|
| 创建子图 | plt.subplot(xyn) |
|
| 创建子图2 | plt.subplots(x,y) |
与上者有一些不同,用一个列表来表示个子图 |
| 创建任意比例的子图 | plt.subplotsgrid(shape,location,rowspan,colspan) |
画图的基本操作
| 功能 | 方法 | 一些解释 |
|---|---|---|
| 折线图 | plt.plot(x,y,'o-',color='') |
第三个为点与线的style |
| 柱形图 | plt.bar(x,y,color='',width=) |
|
| 直方图 | plt.hist() |
|
| 饼图 | plt.pie() |
|
| 散点图 | plt.scatter(x,y,color='',label='') |
|
| 双轴图 | ||
| 等高线 | 见后文 | |
| 场 | 见后文 |
坐标轴和标题的一些处理
| 功能 | 方法 | 一些解释 |
|---|---|---|
| 设置坐标名称(以x为例) | plt.set_xlabel("") |
|
| 设置坐标格式(以y为例) | plt.set_yscale("") |
e.g."log"为指数表示 |
| 设置坐标颜色 | plt.spines[''].set_color("") |
前面的选择有"left","bottom","top","right" |
| 设置坐标粗细 | plt.spines[''].set_linewidth() |
|
| 设置x,y轴范围 | plt.set_xlim(-1,2) |
plt.set_ylim() |
| 设置刻度标签 | plt.set_xticklabels(['haha',0,2,4,'six']) |
|
| 创建图例 | plt.legend(labels=("",""),loc=4) |
loc有1-9的选择 |
一些附加的小操作
| 功能 | 方法 | 一些解释 |
|---|---|---|
| 背景画网格 | plt.grid(color='',ls='',lw=) |
|
| 插入文字 | plt.text(x,y,"",weight="bold",color="") |
|
| 插入带箭头的文字 | plt.annotate("",xy=(),xytext=(),arrowprops=dict()) |
xytext为箭头的vector |
| 插入数学公式 | $\LaTeX$ |
|
| 解决中文乱码问题 | 见后文 |
颜色,点线格式的整理
| 颜色 | 代码 | 点标记 | 代码 | 线型 | 代码 |
|---|---|---|---|---|---|
| 青色 | ‘c’ | 点 | ‘.’ | 实线 | ‘-‘ |
| 品红色 | ‘m’ | 圆圈 | ‘o’ | 虚线 | ‘–’ |
| 黑色 | ‘k’ | ‘X’记号 | ‘x’ | 点虚线 | ‘-.’ |
| 菱形 | ‘D’ | 六角标记 | ‘H’ | ||
| 六角 | ‘H’ | ||||
| 正方形 | ‘s’ | ||||
| 加号 | ‘+’ |
等值线与矢量场
1 | import matplotlib.pyplot as plt |
3D绘图
需要引入matplotlib的第三方工具包mpl_toolkits.mplot3d
感觉和2D的差不多,差不多在画图方法名后加3D就可以了
不过需要注意
1 | #创建3d绘图区域 |
其他的下次再整理了,ddl压身
Animation
细节下次再整理,我也今天刚刚学
1 | # 初始点 |
中文乱码
可以先看这篇文章,目前只看了里面的第一种方法,以后有时间折腾再看第二种。
一些实例
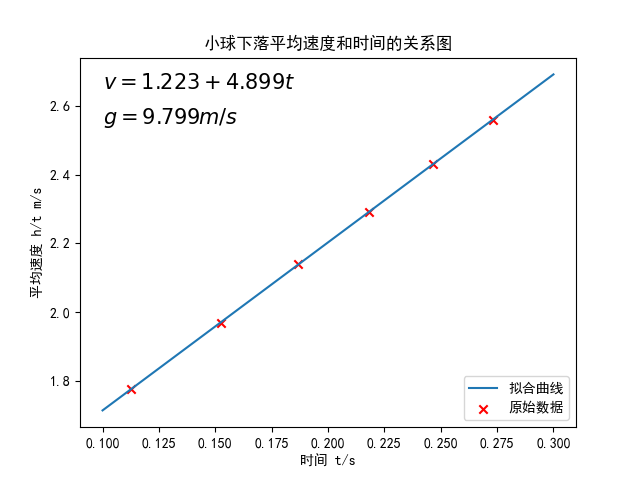
大雾实验重力加速度的曲线拟合
比较简单,随意的附上代码,这个一个初学者也可以写出来。
大概只有知道几个方法就可以写了。
1 | # 2022/3/17 |
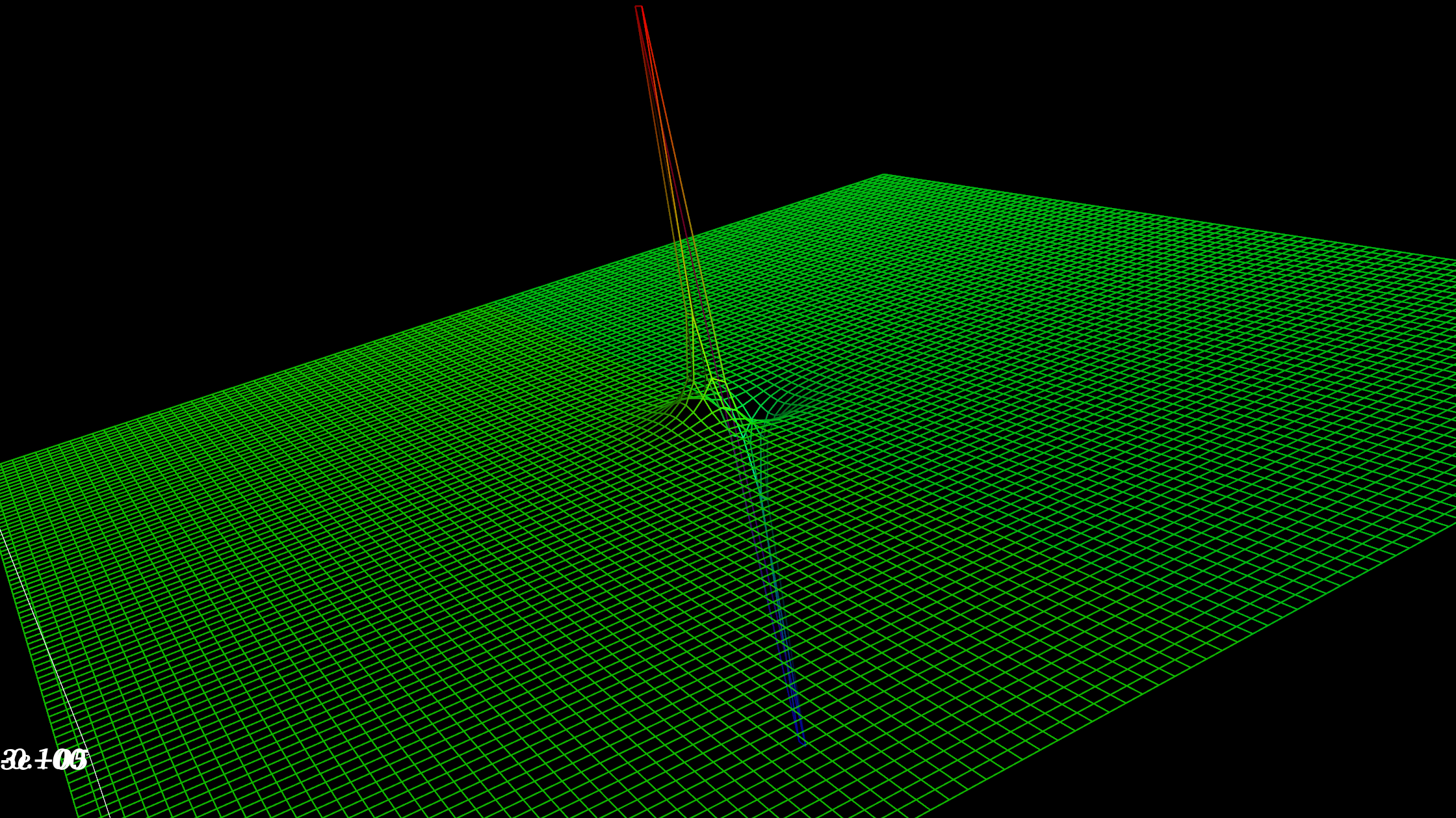
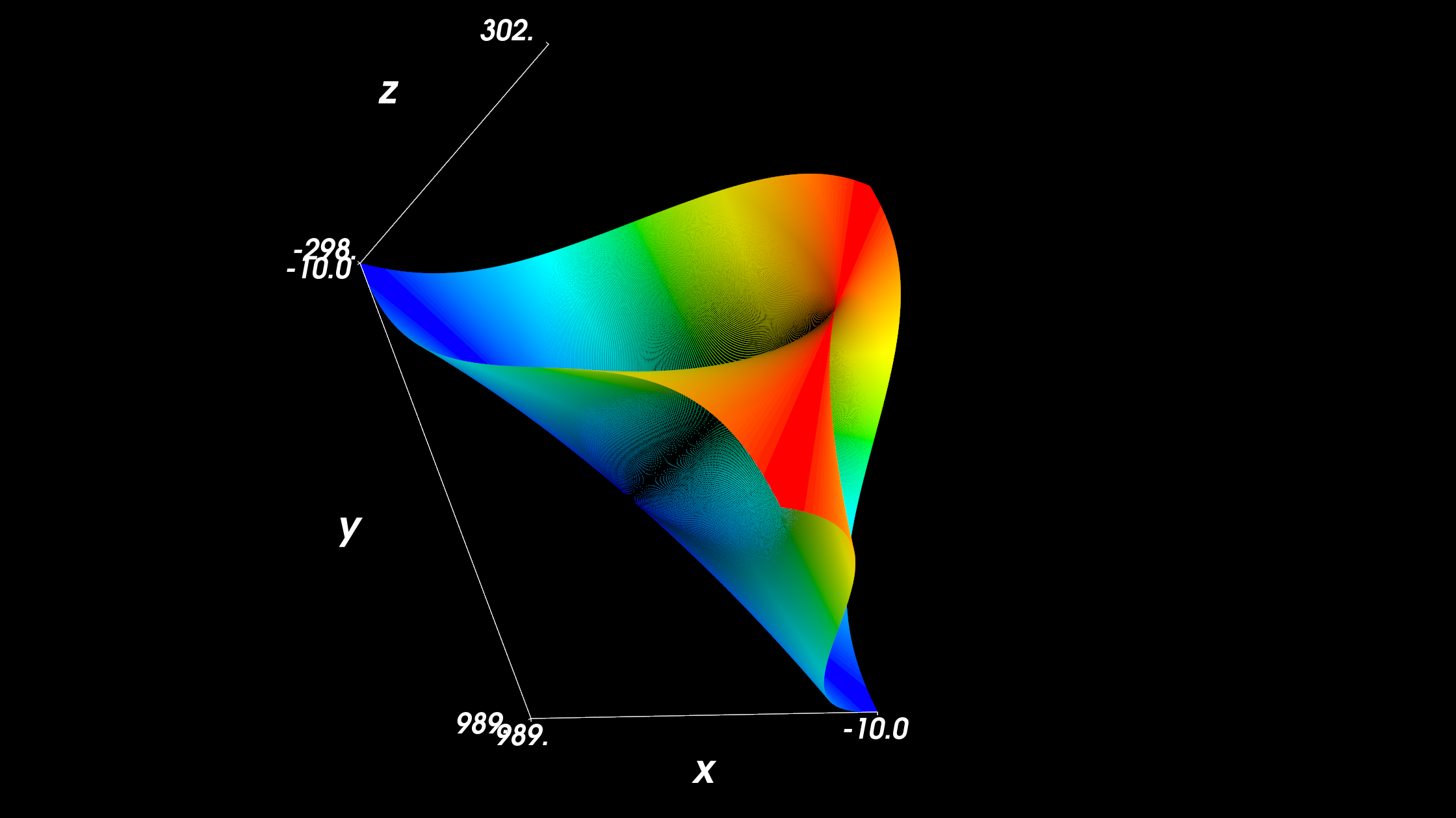
Mayavi画曲面
这个也很简单,不过我没有系统的学习过mayavi,中文资源也比较少。需要进一步整理。
1 | import numpy as np |

- 本文标题:Python科学计算笔记(1)可视化初体验.md
- 本文作者:Chin-ming
- 创建时间:2022-03-22 22:55:50
- 本文链接:https://ck-killer.github.io/blog/2022/03/22/Python科学计算笔记-1-初体验-md/
- 版权声明:本博客所有文章除特别声明外,均采用 BY-NC-SA 许可协议。转载请注明出处!
